パラドックスの森

TOP<<< 予備知識

予備知識

• 場合の数と確率
• 数列・無限等比級数
• 効用

場合の数と確率

事象

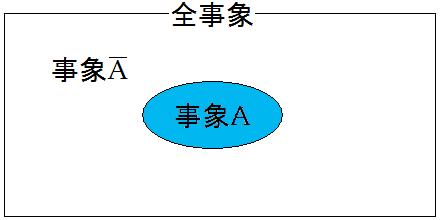
ある確率的試行によって、起こる事柄のことです。例えば、サイコロを振った時に出る目や、コインを投げた時にでる裏表のことです。事象はAやBなどの記号でよく表します。

全事象

ある確率的試行によって、起こるすべての事柄のこと。

余事象

ある事象がおこらない事象のこと。A-やB-などの記号で表します。例えば、サイコロを振って6の目が出る事象をAとすると、1から5の目が6の目が出ない事象であるのでA-となります。

　　　　　　　　　　　　　　　　　　

確率

ある全事象に対して、どれくらいの割合である事象が起こるかを表したもの。記号Pを使って表します。

　　　　　　　　　　　　　　　　　　　　 　P= ある事象が起こる場合の数/全事象の場合の数

　

確率変数、

ある試行を行ったとき、Xという結果が起きてその確率がPであるとき、Xを確率変数と言います。たとえば、サイコロを振った時に出る目、５回勝負して何回勝利するかなどです。

確率分布

確率変数とそれに対応する確率を表にまとめたもの。一般的に以下のような図で表します。

　　　　　　 　　 　　　　　　

確率変数（X）	x1	x2	x3	…	xn-2	xn-1	xn
確率（P）	p1	p2	p3	…	pn-2	pn-1	pn

期待値（平均値）

期待値は試行一回当たりにどれくらいの数字が見込めるかを表す数字です。一般的にE(X)で表します。

期待値は確率変数Xに対して確率Pが存在するとき、次のような式であらわされます。

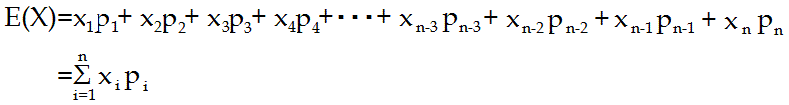
【例1】10円玉を5枚投げて、表になった10円玉は賞金としてもらえるゲームをします。その時のもらえる賞金の確率分布はどうなるかやってみましょう。表の出る枚数は0枚から5枚のいずれかに決まり、もらえる金額は0円から50円の間になります。また、5枚のコインを振った時の出方は全部で2⁵=32通りなので、確率分布は次のようになります。

賞金の確率分布

表の枚数	0	1	2	3	4	5
賞金（X）	0	10	20	30	40	50
確率（P）	1/32	5/32	10/32	10/32	5/32	1/32

10円玉の出方をすべて書き並べたものは、こちらをクリックしてください

【例1】のゲームに参加するには、一回当たり30円の参加費が必要だとします。30円払って参加するのは参加者にとって得でしょうか？このような問題を考える際には、ゲーム一回当たりにいくらの収益が見込めるのか、つまり金額の期待値を求めればよいのです。

上の表を使って期待値を求めると、

E(X)=0×1/32+10×5/32+20×10/32+30×10/32+40×5/32+50×1/32=25(円)

つまり、一回のゲームで期待される収益は25円なので、30円払ってゲームに参加するのは損だということがわかります。

数列・無限等比級数

等比数列

初項(a)に公費(r)を何回も掛け合わせたものを並べて作った数字の列。第n項目の数のことを一般項といい、A_n=ar^n-1であらわします。たとえば、等比数列｛1,2,4,8,16,…,2^n-2,2^n-1,2ⁿ,…｝は初項1、公比2でA_n=1×2^n-1

無限等比級数

ある等比数列を無限に足し合わせたものです。たとえば、等比数列｛1,2,4,8,16,…,2^n-2,2^n-1,2ⁿ,…｝があるとします。このときの無限等比級数は、

1+2+4+8+16+…+2^n-2+2^n-1+2ⁿ+…

です。このとき無限等比級数の和を求めると、無限大(∞)となります。無限等比級数が±∞になることを発散するといいます。

無限等比級数の収束

無限等比級数で収束するというと、無限等比級数の和がある一定の値に収まるということです。一般項がA_n=ar^n-1の無限等比級数が/r/<1【-1

　　　　　　 S=a/1-r

です。

たとえば、等比数列{1,1/2,1/4,1/8,1/16,…,1/2^n-2,1/2^n-1,1/2ⁿ,…}があるとします。このとき、一般項A_n=1×1/2^n-1です。無限等比級数の和Sは、

　 S=a/1-r=1/(1-1/2)=2

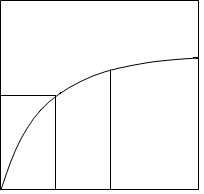
で2に収束します。

効用

限界効用

私たちはおいしいものを食べたり、ゲームをやったりすると満足度を得ます。この満足度のことを効用と言います。一方で限界効用は、モノを一単位追加するときに得られる満足度(限界効用)のことです。効用はモノを追加するほど増えますが、限界効用は逓減することに注意しなくてはなりません。

たとえば、私が今腹ぺこでリンゴを何個か食べることとします。最初の一個を食べるとき、私は大きな満足度を得ることができます。しかし、二個目を食べるときには、一個目のリンゴに比べたら小さな満足度しか得られないでしょう。なぜなら、すでにリンゴを一個食べており、そのためある程度お腹が満たされているからです。下の図をご覧ください。これは、リンゴをX個食べる時に得られる効用をUをU=X^1/2とした時のグラフです。

限界効用はグラフでは効用関数の接線の傾きで表わされます。グラフからわかるとおり、リンゴを食べるほどこの傾きはどんどん減少します。つまり、限界効用は減っているのです。

TOP<<< 予備知識